每年参加中考得到同学都会问“今年中考难不难”?中考考试还没有来,更本不知道难还是不难,而且每年各科的考试题目都不一样,不过都是围绕着初中三年的知识点出考题,所以同学们上课时要做好课堂笔记,多复习知识点,特别是数学和化学公式,只要记住了公式,那么做题就不是问题。想要交一份满意的中考答卷,得全靠自己努力,下面是小编分享的部分2018年数学模拟题,仅供参考。
2018年贵阳中考数学模拟试题
一、填空题
1.已知:a﹣2的值是非负数,则a的取值范围为.
2.如图,王老师在上多边形外角和这节课时,做了一个活动,让小明在操场上从A点出发前进1m,向右转30°,再前进1m,又向右转30°,…,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.小明一共走了m,这个多边形的内角和是度.
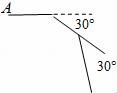
3.如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为![]() .⊙P运动一圈与△OBC的边相切次,每次相切时,点P到等边三角形顶点最近距离是.
.⊙P运动一圈与△OBC的边相切次,每次相切时,点P到等边三角形顶点最近距离是.
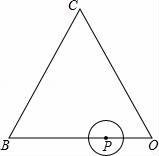
4.已知点A(x1,y1),B(x2,y2)是反比例函数y=﹣![]() 的图象上的两点,若x1<0(填“>”或“<”或“=”) 5.如图,在反比例函数y=
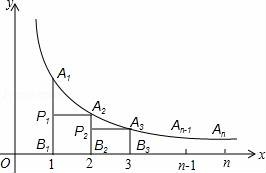
的图象上的两点,若x1<0(填“>”或“<”或“=”) 5.如图,在反比例函数y=![]() (x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn=.
(x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn=.
二、解答题
6.先化简,后求值:![]() ,再任选一个你喜欢的数x代入求值.
,再任选一个你喜欢的数x代入求值.
7.“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.

8.中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

9.某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其它区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
10.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2![]() ,求正方形ADCE周长.
,求正方形ADCE周长.

11.某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
①甲队单独完成此项工程刚好如期完工;②乙队单独完成此项工程要比规定工期多用5天;③若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
如果工程不能按预定时间完工,公司每天将损失3000元,你觉得哪一种施工方案最节省工程款,并说明理由.
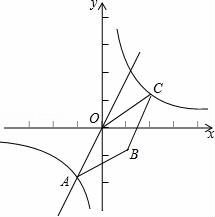
12.如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
13.如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+![]() +BB′为最短路线(其中AA′,BB′都与⊙O相切).
+BB′为最短路线(其中AA′,BB′都与⊙O相切).
(1)你能计算出这段公路的长度吗?(结果精确到0.1km)
(2)阴影部分的面积是多少?(结果精确到1km2)
14.如图①,将一张直角△ABC纸片折叠,使点A与点C重合,这时DE为折痕,△ECB为等腰三角形;继续将纸片沿△ECB的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的矩形为“叠加矩形”.
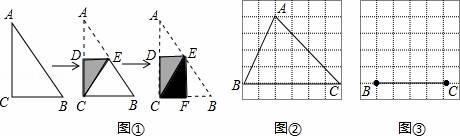
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕.
(2)如图③在正方形网格中,以给定的BC为一边,画出一个斜三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
(3)若一个三角形所折成的“叠加矩形”为正方形,那么必须满足的条件是什么?
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是什么?
15.如图,已知抛物线y=﹣![]() +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
(1)求抛物线的解析式及其对称轴方程.
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.
(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D的坐标和△DBC的面积;若不存在,请说明理由.

小编总结
中考来临的前期,校园里充满了紧张的氛围。而在这个阶段里,是考生们复习的黄金时期,各科的教学都基本结束了,老师们也将进行一、二论总复习。把繁杂的知识系统化、条理化,找到每科中的一条宏观的线索,提纲挈领,全面复习。巧用错题集、往年中考和模拟真题。查找知识漏洞,进行专项突破。
展开全文 ∨




